In data structure, we often need to rearrange elements of our data on basis of increasing/decreasing order to perform our key operation. This process of rearrangement is called sorting. There are multiple ways to make this rearrangement possible, and they are known as sorting algorithms in data structure.
Sorting algorithms in Data Structure
In this article, we are going to cover main sorting algorithms used in data structure. All the code implementation has been done in Python language.
- Bubble Sort
- Merge Sort
- Insertion Sort
- Quick Sort
- Selection Sort
- Heap Sort
Bubble sort
Bubble sort is simplest of all the sorting algorithms. In bubble sort, we compare each element with its adjacent neighbor and swap if it bigger.
Pseudo code of bubble sort
- Iterate over list
- If element is greater than next element, then swap
- Re-iterate over list

Figure: Bubble sort
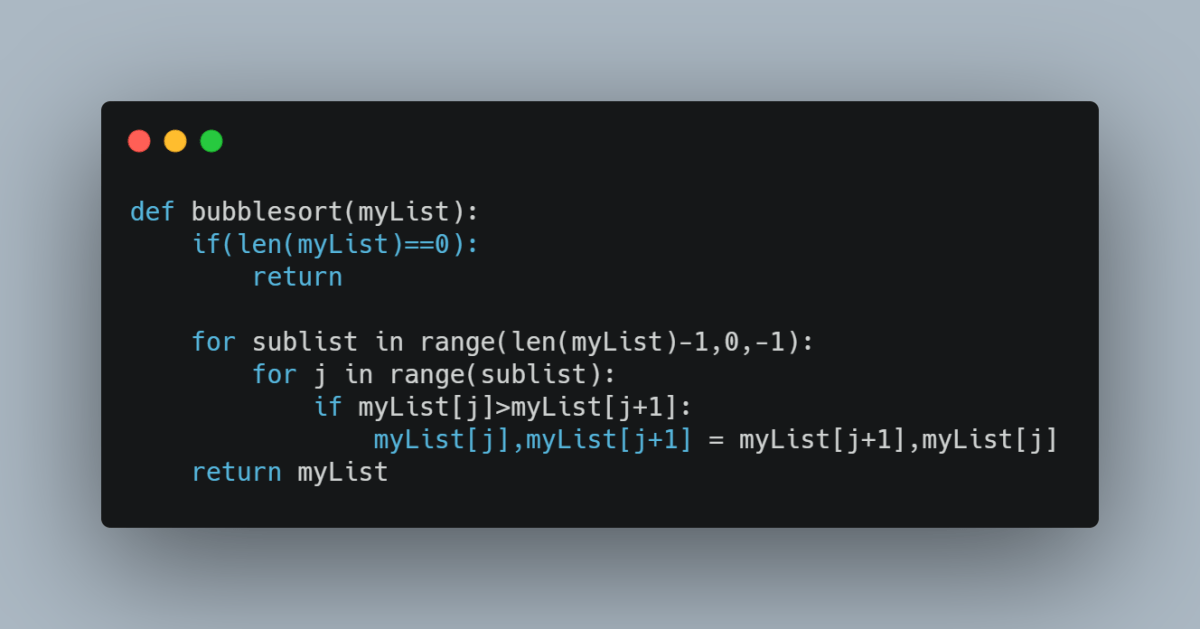
Figure: Python code for bubble sort
Merge Sort
Merge sort is based upon divide and conquer technique. In merge sort, we divide recursively divide each sub-lists into element level, and then start merging them.
Pseudo code for merge sort
- Recursively divide list into 2 halves, till we have each list with single elements
- Now, start comparing and merging each of these list .
- Keep doing this till we have complete list

Figure: Merge Sort

Figure: Python code for Merge sort
Insertion Sort
Insertion sort is in place comparison algorithm. Here we are creating a sub-list of sorted elements from our given list, and iteratively keep on adding new elements and sort them.
Pseudo code of Insertion sort
- Iterate over list starting from beginning
- Create a sub-list, by pushing new element from our list
- Sort this sub-list
- Do this till we reach end

Figure: Insertion Sort

Figure: Python code for Insertion sort
Quick Sort
Quick sort is highly efficient sorting algorithm which is often used for large data sets. Quick sort is based upon partitioning list into smaller lists (based on pivot point). Elements are arranged on basis of whether they are smaller or larger than pivot.
This algorithm is quite efficient for large-sized data sets as its worst-case complexity is O(nLogn).
Pseudo code of quick sort
- Choose the highest index value has pivot
- Take two variables to point left and right of the list excluding pivot
- left points to the low index
- right points to the high
- while value at left is less than pivot move right
- while value at right is greater than pivot move left
- if both step 5 and step 6 does not match swap left and right
- if left ≥ right, the point where they met is new pivot

Figure: Quick Sort

Figure: Python implementation of Quick sort
Selection Sort
Selection sort is simplest of sorting algorithm. Selection sort is an in place comparison where we will keep iterating and building sorted new list from our given data. The smallest element is selected from the unsorted array and swapped with the leftmost element, and that element becomes a part of the sorted array. This process continues moving unsorted array boundary by one element to the right. Selection sort is not an efficient sorting method and is not used for larger data set. Its worst order complexity is square(n).
Pseudo code of Selection Sort
- Set max or min to location 0 or last
- Search the minimum element in the list
- Swap with value at location min/max
- Increment max/min to point to next element
- Repeat until list is sorted

Figure: Selection Sort

Figure: Python implementation of selection sort
Heap Sort
Heap sort is similar to selection sorting where we find maximum or minimum element and place it in end iteratively. Heap sort algorithm is comparison based sorting algorithm. Heap sort is based upon binary heap data structure.
Binary heap is data structure where elements are stored in pyramid based structure and parent elements are larger than child nodes (max heap) or smaller than child nodes (min heap).
Pseudo code of Heap sort
- Build a max heap from the list data
- At this point, the largest item is stored at the root of the heap. Replace it with the last item of the heap followed by reducing the size of heap by 1. Finally, heapify the root of tree.
- Repeat above steps while size of heap is greater than 1.

Figure: Heap Sort

Figure: Python implementation of heap sort
Time complexity comparison of various sorting algorithms
| Sorting Algorithm | Time Complexity (n is list size) |
| Bubble Sort | Square(n) |
| Merge Sort | nlog(n) |
| Insertion Sort | Square(n) |
| Quick Sort | nlog(n) |
| Selection Sort | Square(n) |
| Heap Sort | nlog(n) |
As we can see best sorting algorithms are Merge Sort , Quick Sort and Heap Sort (on basis of worst case performance.
Sorting algorithm interview questions
Sorting algorithms based questions are asked directly in the tech companies interviews.
- When does the worst case of QuickSort occur?
- Given a big string of characters, how to efficiently find the first unique character in it?
- How to count inversions in a sorted array?
- Given a big array, how to efficiently find k’th largest element in it?
- Implement the Bubble sort Algorithm?
- How is an iterative quicksort algorithm implemented?
- How do you implement a counting sort algorithm?
- How do you implement an insertion sort algorithm?
- How is a merge sort algorithm implemented?
- How do you implement a bucket sort algorithm?
- Selection Sort Algorithm
- Iterative Merge Sort Algorithm (Bottom-up Merge Sort)
- QuickSort Algorithm
- Iterative Implementation of QuickSort
- Hybrid QuickSort
- QuickSort using Dutch National Flag Algorithm
- QuickSort using Hoare’s Partitioning scheme
- Heap Sort Algorithm
- Introsort Algorithm
- External Merge Sort Algorithm
- Counting Sort Algorithm
- Inversion Count of an array
- Sort an array using Young tableau
- Merge Sort Algorithm for Singly Linked List
- Problems solved using partitioning logic of QuickSort
- Sort a Doubly Linked List using Merge Sort
- Sort elements by their frequency and Index
- Sort an array based on order defined by another array
- Efficiently sort an array with many duplicated values
- Find largest number possible from set of given numbers
- Find the surpasser count for each element of an array
- Segregate positive and negative integers using Merge Sort
- Group anagrams together from given list of words
- How is an integer array sorted in place using the quicksort algorithm
- How do you find the largest and smallest number in an unsorted integer array?
End Note
In this article, we have covered important sorting algorithms in the data structure. Sorting based problems are frequently asked in interviews like Google, Amazon etc. It is very important to know them, and see how they are implemented. We have shared the python implementation of each of sorting algorithms.
If you have any doubt or suggestion, please feel free to reach us. You can post in discussion thread below or write to us at info@xamnation.com
We are offering online course for technical interview preparation. We have courses on learning programming languages, preparing for aptitude tests, learning data structure and algorithms and mock interview preparation. Connect with us at info@xamnation.com if you are looking for any help.
You may like to see

